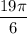Question

Use the shell method to find the volume of the solid generated by revolving the regions bounded by the curves and lines about the y-axis.y = x^2 , y = 9-8x , x=0, for x greater than or equal to 0The Volume is ?(Type an exact answer in terms of pi)Each step would be nice

Answer 1

The volume of the solid is:

`\displaystyle(19\pi)/(6)`

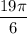
Explanation:

See the graph of the region attached.

To find the intersection between the line and the parabola we set the equation equal to each other, and solve that quadratic equation by factorization:

`x^2=9-8x\\x^2+8x-9=0\\(x+9)(x-1)=0\\x=-9,x=1`

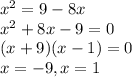
Since the region is the one for
`x\ge 0` then the intersection we are interested on is x=1 as it can also be seen in the graph.

Then we set the integral using shell method for revolving about the y-axis:

`\displaystyle\int_a^b 2\pi\,x\,h(x)\,dx`

Where h(x) is the height of the shell which here is the distance between the parabola and the line, so
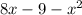`8x-9-x^2` (since the line is on the top we subtract from it the parabola)

Then the integral becomes:

`\displaystyle\int_0^1 2\pi\,x\,(8x-9-x^2)\,dx`

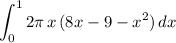
Notice the limits of the integral are the x-axis (x=0) and the intersection of the parabola and the line that we found before (x=1)

Now, solving the integral:

Start by factoring the
`2\pi` and distributing the x:

`=\displaystyle2\pi \int_0^19x-8x^2-x^3dx`

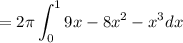
Then use the basic rule to integrate:

`=\displaystyle2\pi \left[(9x^2)/(2)-(8x^2)/(3)-(x^4)/(4)\right|_0^1`

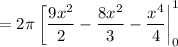
Then evaluate the antiderivative in the limits and subtract:

`=\displaystyle2\pi\left[(9)/(2)-(8)/(3)-(1)/(4)-0\right]=(19\pi)/(6)`

So the volume of the solid is
`\displaystyle(19\pi)/(6)`