Question

A light-rail commuter train accelerates at a rate of 1.35 m/s2. How long does it take to reach its top speed of 80.0 km/h, starting from rest? The same train ordinarily decelerates at a rate of 1.65 m/s2. How long does it take to come to a stop from its top speed? In emergencies the train can decelerate more rapidly, coming to rest from 80.0 km/h in 8.30 s. What is its emergency deceleration in m/s2?

Answer 1

16.46 seconds.

13.46 seconds

2.67 m/s²

Step-by-step explanation:

Acceleration = a = 1.35 m/s²

Final velocity = v = 80 km/h =
`80(1000)/(3600)=(200)/(9)\ m/s`

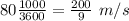
Initial velocity = u = 0

Equation of motion

`v=u+at\\\Rightarrow (200)/(9)=0+1.35t\\\Rightarrow t=((200)/(9))/(1.35)=16.46\ s`

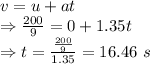
Time taken to accelerate to top speed is 16.46 seconds.

Acceleration = a = -1.65 m/s²

Initial velocity = u = 80 km/h=
`80(1000)/(3600)=(200)/(9)\ m/s`

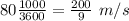
Final velocity = v = 0

`v=u+at\\\Rightarrow 0=(200)/(9)-1.65t\\\Rightarrow t=((200)/(9))/(1.65)=13.46\ s`

Time taken to stop the train from top speed is 13.46 seconds

Initial velocity = u = 80 km/h=
`80(1000)/(3600)=(200)/(9)\ m/s`

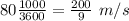
Time taken = t = 8.3 s

Final velocity = v = 0

`v=u+at\\\Rightarrow 0=(200)/(9)+a8.3\\\Rightarrow a=(-(200)/(9))/(8.3)=-2.67\ m/s^2`

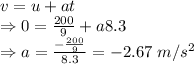
Emergency deceleration is 2.67 m/s²