Question

Person A leaves his home to visit his cousin, person B who lives 76 miles away. He travels at an average rate of 44 miles per hour. One half hour later person B leaves her house to visit person A traveling at an average rate

of 64 miles per hour. How long after person B leaves will it be before they meet?

Answer 1

There are going to meet half a hour after person B leaves.

Explanation:

The first step to solve this problem is model the position equation for both person A and person B. It can be done by a first order equation.

I am going to say that the positive direction is from the person A to the person B. So, A starts at the position 0 and B at the position 76.

The first step is to find the equation of the position of person A

The initial position of A is 0 and he travels 44 miles per hour in the direction of B, so to the positive diretion. So, the position S of person A is

`S_(A)(t) = 44t`,

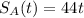where t is the time in hours.

Now we have to find the equation of the position of person B

The initial position of B is 76 and he travels 64 miles per hour in the direction A, so in the negative direction. The position S of person B is

`S_(B)(t) = 76 - 64t`

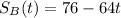
Now we have to restart the time from the moment the person B leaves her house.

It happens at 0.5h, at this moment the person A is at the position

`S_(A)(0.5) = 44*(0.5) = 22`

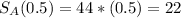
So, from this moment, the equation of the position of A is:

`S_(A)(t) = 22 + 44t`

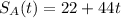
They will meet at the instant t when

`S_(A)(t) = S_(B)(t)`

`22 + 44t = 76 - 64t`

`108t = 54`

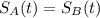
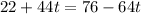
t = 0.5h

There are going to meet half a hour after person B leaves.