Answer:
Part a)
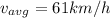
Part b)
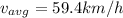
Part c)
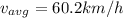
Part d)
average velocity must be ZERO
Step-by-step explanation:
While he drive San Antonio to Houston
Half the time move with speed 51 km/h and next half his speed is 71 km/h
so we have

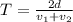
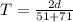
so average speed is given as
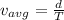
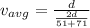
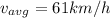
Part b)
While he move from Houston to San Antonio half the distance is moved with 51 km/h and next half distance with 71 km/h
so we have
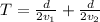
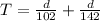
so average speed is given as
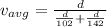
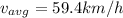
Part c)
Average speed for entire trip
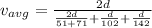
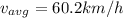
Part d)
Since total displacement of entire trip is zero
so average velocity must be ZERO