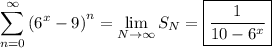Question

I found the interval of convergence, but I am not sure how to do the second part, finding the sum of the series as a function of x.

Answer 1

The given series is geometric with common ratio
`6^x - 9`, which converges if
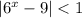`|6^x - 9|<1` (i.e. the interval of convergence). We have the well-known result

`\displaystyle |r| < 1 \implies \sum_(n=0)^\infty ar^n = (a)/(1-r)`

If you're not familiar with that result, it's easy to reproduce.

Let
`S_N` be the
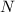`N`-th partial sum of the infinite series,

`\displaystyle S_N = \sum_(n=0)^N \left(6^x - 9\right)^n = 1 + \left(6^x - 9\right) + \left(6^x - 9\right)^2 + \cdots + \left(6^x - 9\right)^N`

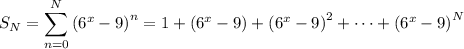
Multiply both sides by the ratio.

`\left(6^x - 9\right) S_N = \left(6^x - 9\right) + \left(6^x - 9\right)^2 + \left(6^x - 9\right)^3 + \cdots + \left(6^x - 9\right)^(N+1)`

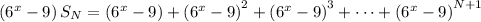
Subtract this from
`S_N` to eliminate all the powers of the ratio between 0 and
`N+1`.

`\left(1 - \left(6^x - 9\right)\right) S_N = 1 - \left(6^x - 9\right)^(N+1)`

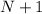Solve for
`S_N`.

`S_N = (1 - \left(6^x - 9\right)^(N+1))/(10-6^x)`

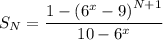
Now as
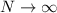`N\to\infty`, the exponential term converges to 0 and we're left with

`\displaystyle \sum_(n=0)^\infty \left(6^x-9\right)^n = \lim_(N\to\infty) S_N = \boxed{\frac1{10-6^x}}`