18 is even, so by rule (a) cosmological, let's call it C. 18 is real and C and so by (b) not mystical, not M.
So V2 which I guess is
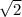 is our only hope.
is our only hope.
Assume
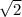 is not M.
is not M.
Then
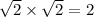 is M, as by (c) it's the product of two not M numbers.
is M, as by (c) it's the product of two not M numbers.
2 is even, so 2 is C (rule (a)). So 2 is not M (rule (b)). That's a contradiction.
Therefore our assumption is false. We conclude
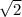 is mystical.
is mystical.