Question

(22) Let A be a 100 x 90 matrix, representing an image with 9000 pixels. How many numbers do we need to store for a truncated singular value decompo- sition (TSVD) A = Ak with k = 10 ? (a) 1090 (b) 1900 (c) 1910 (d) 1990 (e) 2018

Answer 1

The correct option is c.

Explanation:

Let A be a 100 x 90 matrix.

The order of a matrix is m x n, where, m is number of rows and n is number of columns.

`m=100`

`n=90`

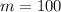
It is given that for a truncated singular value decompo- sition (TSVD)
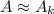`A\approx A_k` with k=10.

The formula for the number of numbers do we need to store for a truncated singular value decompo- sition (TSVD)
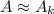`A\approx A_k` is

`N=k(m+n+1)`

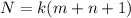
Substitute k=10, m=100 and n=90 in the above formula.

`N=10(100+90+1)`

`N=10(191)`

`N=1910`

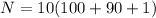
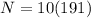
The numbers that are needed to store for a truncated singular value decompo- sition (TSVD) is 1910.

Therefore the correct option is c.