Question

If one quantity Z is a function of two other quantities X and Y , Z = Z(X, Y ), then their derivatives with respect to each other are related as ∂X ∂Y Z ∂Y ∂Z X ∂Z ∂X Y = −1.

Answer 1

It is given that, One Quantity Z is a function of two other quantities X and Y such that

Z=Z(x,y)

Taking Partial Derivative of Z with respect to x and y ,and then partial derivative of x with respect to y,and then Multiplying the three equations, we get

`\rightarrow1=y* (\partial x)/(\partial z)----(1)\\\\\rightarrow1=x* (\partial y)/(\partial z)----(2)\\\\\rightarrow x* (\partial y)/(\partial x)+y=0\\\\\rightarrow (\partial y)/(\partial x)=(-y)/(x)------(3)\\\\1 * 2 * 3\\\\\rightarrow (\partial x)/(\partial y) * (\partial y)/(\partial z) * (\partial z)/(\partial x)=(-x)/(y) * (1)/(x) * y\\\\= -1`

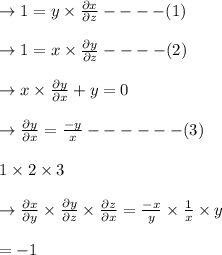
Cancelling terms from numerator and Denominator to Obtain the result.