Question

A machine shop has 100 drill presses and other machines in constant use. The probability that a machine will become inoperative during a given day is 0.002. During some days no machines are inoperative, but during other days, one, two, three or more are broken down. The probability of their break down number follows Poisson distribution. What is the probability that fewer than two machines will be inoperative during a particular day?

Answer 1

The probability is 0.9824

Explanation:

If a variable x follows a poisson distribution, the probability P is given by:

`P(x)=(e^(-λ)*λ^(x))/(x!)`

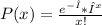
Where x counts the number of events that happens in a specific time and λ is the mean number of events in that specific time.

So, if the probability that a machine will become inoperative during a given day is 0.002 and there are 100 drill presses, then the value of λ or the mean is calculated as:

λ = 100*0.002 = 0.2

Then, the probability that fewer than two machines will be inoperative during a particular day is:

P(x<2) = P(x=0) + P(x=1)

`P(x<2)=(e^(-0.2)*0.2^(0))/(0!)+(e^(-0.2)*0.2^(1))/(1!)`

P(x<2) = 0.8187 + 0.1637

P(x<2) = 0.9824

Finally, the probability that fewer than two machines will be inoperative during a particular day is 0.9824