Answer:
y = (-1,1)
Explanation:
If a point y
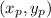 divides a line A
divides a line A
 B
B
 in the ratio a:b, the formula to find the coordinates of the point y is:
in the ratio a:b, the formula to find the coordinates of the point y is:
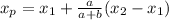
and
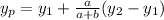
We know Point A is (-3,4) and Point B is (3,-5). And the ratio is a:b or 1:2, so we can say:
 = -3
= -3
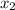 = 3
= 3
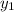 = 4
= 4
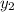 = -5
= -5
a = 1
b = 2
Plugging these into the formula, we get:

and
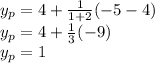
So the point y is (-1,1)