Question

Find the measure of an exterior angle of a regular polygon with 19 sides.

Answer 1

The measure of the exterior angle is 18. 95 Degrees.

Explanation:

Step 1:

Given data:

Let us assume ‘I’ as interior angle of Regular polygon and ‘E’ as Exterior angle of Regular Polygon.

Exterior angle for Regular polygon is 19 sides.

By the formula:

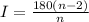`I=(180(n-2))/(n)` degrees. ------1.n(s) is the side of polygon.

Step 2:

Substitute the value of n in the given formula. Where n=19 from the given data

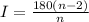`I=(180(n-2))/(n)`degrees

Step 3:

`\begin{array}{l}{I=(180(19-2))/(19) \text { degrees }} \\ {I=(180(17))/(19) \text { degrees }}\end{array}`

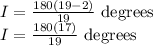
I = 3060/19

I = 161.05 degrees.

Step 4:

Measure of the exterior angles of a regular polygon is given by the formula:

E= 360 / n degrees. ----- n(s) side of polygon.

From the given data n are 19.

E = 360 / 19

E= 18. 95 Degrees.

Answer 2

Answer:
`18.94\°`

Explanation:

The exterior angle of a regular polygon of
`n` sides is given by:

`(360\°)/(n)`

In the case of a 19-side polygon
`n=19`

Hence:

`(360\°)/(19)=18.94\°`