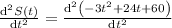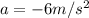Question

A ball is thrown from the top of a building. At time t (in seconds), its height (in feet) follows the path s(t) = -3t2 + 24t + 60.

a. When does it hit the ground?
b. What was its acceleration at time t = 1 ?

Answer 1

Answer:10 sec

Step-by-step explanation:

Given

Ball follows the path
`S(t)=-3t^2+24t+60`

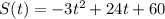
Therefore at t=0

S(0)=60

i.e. height of building is 60 m

(a)Ball will hit when the distance between ball and ground is zero i.e.

`0=-3t^2+24t+60`

`3t^2-24t-60=0`

`t^2-8t-20=0`

`t^2-10t+2t-20=0`

`\left ( t+2\right )\left ( t-10\right )=0`

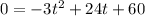
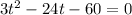
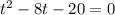
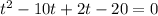
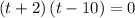
i.e. at t=10 sec ball will hit ground

(b)accleration at time t=1 sec

acceleration is given by
`\frac{\mathrm{d^2} S(t)}{\mathrm{d} t^2}=\frac{\mathrm{d^2} \left ( -3t^2+24t+60\right )}{\mathrm{d} t^2}`

`a=-6 m/s^2`