Question

• (10 pts) Prove that the relation S= {(x,y) E RR:x^2=y^2} is reflexive on R. symmetric and transitive.

Answer 1

Explanation:

Given that S is a relation in R such that

x,y is related if

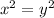`x^2=y^2` for x,y real numbers

For any real number we have

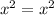`x^2=x^2` hence S is reflexive

Similarly whenever

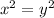`x^2=y^2` we get

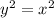`y^2=x^2` Hence symmetric

When
`x^2=y^2 and\\y^2=z^2`

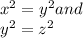
we get

`x^2=z^2`

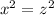
Thus transitive

Thus we find that S is reflexive, symmetric and transitive on R