Answer:
For every n E N, when we divide n² by 7, the remainder is either 0, 1, 2, or 4.
Explanation:
Given information: n∈N and
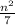 .
.
To prove: For every n E N, when we divide n2 by 7, the remainder is either 0, 1, 2, or 4.
Proof:
Using basic remainder remainder theorem,
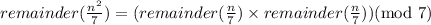
where, mod 7 is modulo 7. It means the remainder after dividing by 7.
If a natural number divide by 7 then the possible remainders are 0,1,2,3,4,5 and 6.
If remainder of n/7 is 0, then
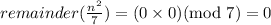
If remainder of n/7 is 1, then
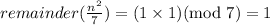
If remainder of n/7 is 2, then
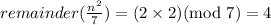
If remainder of n/7 is 3, then
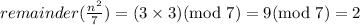
If remainder of n/7 is 4, then
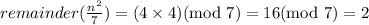
If remainder of n/7 is 5, then
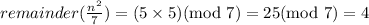
If remainder of n/7 is 6, then
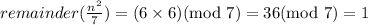
For every n E N, when we divide n2 by 7, the remainder is either 0, 1, 2, or 4.
Hence proved.