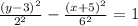Question

Write the equation of a hyperbola with a center at (-5, -3), vertices at (-5, -5) and (-5, -1) and co-vertices at (-11, -3) and (1, -3).

Answer 1

The equation of this hyperbola is

`((y-3)^2)/(2^2) -((x+5)^2)/(6^2) =1`

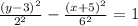
Explanation:

Given from the question,

center of hyperbola (h,k) is (-5,3)

vertices of hyperbola are at (-5,-5) and ( -5,-1)

You know the length of the transverse is 2a, and can be found using the vertices given as -1--5=4

2a=4, hence a=4/2 =2

a=2

The coordinates of the co-vertice are (-11,-3) and (1,-3)

You know the length of the conjugate axis is 2b and can be found using the co-vertices given as 1--11=12

12=2b,

b=6

The standard equation of a hyperbola with center h,k and transverse axis parallel to the y-axis is

`((y-k)^2)/(a^2) -((x-h)^2)/(b^2) =1`

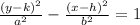
substitute values as

`((y-3)^2)/(2^2) -((x+5)^2)/(6^2) =1`