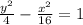Question

Write the equation of a hyperbola with vertices (0, -2) and (0, 2) and co-vertices (-4, 0) and (4, 0).

y squared/16 minus x squared/4 equals 1

x squared/4 minus y squared/16 equals 1

y squared/4 minus x squared/16 equals 1

x squared divided by 16 minus y squared divided by 4 equals 1

Answer 1

C. y squared/4 minus x squared/16 equals 1

Explanation:

Given that vertices of hyperbola are (0,-2) and (0,2) and

Co-vertices of hyperbola as (-4,0) and (4,0) then a sketch will show you that this hyperbola has its transverse axis on the y-axis and has its center at the origin (0,0)

This means that the standard equation for the hyperbola should follow;

`(y^2)/(a^2) -(x^2)/(b^2) =1`

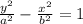
Using the coordinates of the vertices, you can find the length of the transverse axis and the value of a as;

(0,-2) and (0,2) , 2--2=4

2a=4

a=4/2=2

a=2

Using the coordinates of the co-vertices, you can find the length of the conjugate axis as;

(-4,0) and (4,0) ⇒ 4--4=8

2b=8

b=8/2=4

b=4

substitute values in equation as;

`(y^2)/(4) -(x^2)/(16) =1`