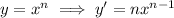Question

How to differentiate y=x^n using the first principle. In this question, I cannot use the rule of differentiation. I have to do the old fashioned way. How do I do it?​

Answer 1

By first principles, the derivative is

`\displaystyle\lim_(h\to0)\frac{(x+h)^n-x^n}h`

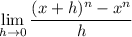
Use the binomial theorem to expand the numerator:

`(x+h)^n=\displaystyle\sum_(i=0)^n\binom nix^(n-i)h^i=\binom n0x^n+\binom n1x^(n-1)h+\cdots+\binom nnh^n`

`(x+h)^n=x^n+nx^(n-1)h+\frac{n(n-1)}2x^(n-2)h^2+\cdots+nxh^(n-1)+h^n`

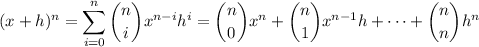
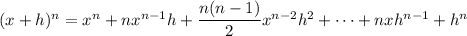
where

`\dbinom nk=(n!)/(k!(n-k)!)`

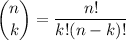
The first term is eliminated, and the limit is

`\displaystyle\lim_(h\to0)\frac{nx^(n-1)h+\frac{n(n-1)}2x^(n-2)h^2+\cdots+nxh^(n-1)+h^n}h`

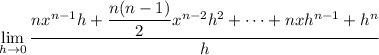
A power of
`h` in every term of the numerator cancels with
`h` in the denominator:

`\displaystyle\lim_(h\to0)\left(nx^(n-1)+\frac{n(n-1)}2x^(n-2)h+\cdots+nxh^(n-2)+h^(n-1)\right)`

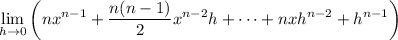
Finally, each term containing
`h` approaches 0 as
`h\to0`, and the derivative is

`y=x^n\implies y'=nx^(n-1)`