Question

Using a geometric growth model to predict population growth, a population of 10 individuals at time zero with a finite growth rate (X?, lambda?, lambda) of 1.4 would be expected to exceed 500 in how many years?

A. 7
B. cannot calculate from the information given
C. 10
D. 16
E. 12
F. 21

Answer 1

Answer: Option E, in 12 years.

Step-by-step explanation:

A geometric growth model is characterized by its finite growth rate, known as lambda. The size of the population after a unit of time has passed can be calculated using the last known size and lamba as:

`N_(t+1) = \lambda * N_t`

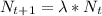
Starting from the initial value of population, the next one will be calculated multiplying by 1.4, and the next one multiplying again by 1.4, thus we can define a function that relates the time passed in year to the size of the population:

`N(t) = \lambda^(t) *N_0`

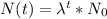
Substituting our values we get the function that defines the growth of our poupulation:

`N(t) = 1.4^(t) *10`

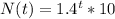
Then, we just have to clear the t that gives a population of 500:

`500 =  1.4^t*10, divide\ both\ sides\ by\ 10\\50 = 1.4^t, apply\ log_(1.4)(x)\ to\ both\ sides\\log_(1.4)(50)=t\\11.63=t`

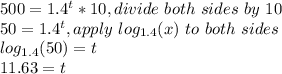
Thus, at 12 years, the population will be greater than 500.