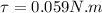Question

A 200-turn rectangular coil having dimensions of 3.0 cm by 6.0 cm is placed in a uniform magnetic field of magnitude 0.76 T. (a) Find the current in the coil if the maximum torque exerted on it by the magnetic field is 0.14 N · m. A (b) Find the magnitude of the torque on the coil when the magnetic field makes an angle of 25° with the normal to the plane of the coil. N · m

Answer 1

(a). Current, I = 0.512 A = 512 mA

(b). Torque,
`\tau = 0.059 N.m`

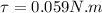
Given:

Number of turns in the rectangular coil, n = 200 turns

Area of the coil with dimensions 3.0 cm by 6.0 cm, A =
`3.0* 6.0 = 18.0 cm^(2) = 18.0* 10^(- 4) m^(2)`

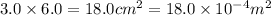
Intensity of magnetic field, B = 0.76 T

maximum torque,
`\tau_(max) = 0.14 N.m.A`

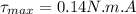
angle,
`\theta = 25^(\circ)`

Solution:

(a) Current in the coil, I can be calculated by the given relation:

`\tau_(max) = nABI`

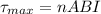
Therefore,

`I = (\tau_(max))/(nAB)`

Now substituting the given values in the above eqn:

`I = (0.14)/(200* 18.0* 10^(-4) * 0.76)`

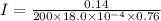
I = 0.512 A = 512 mA

(b) Magnitude of torque can be calculated by the given relation:

`\tau = \tau_(max)sin\theta`

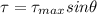
Now,

`\tau = 0.14* sin25^(\circ)`

`\tau = 0.059 N.m`