Question

In an attempt to escape his island, Gilligan builds a raft and sets to sea. The wind shifts a great deal during the day, and he is blown along the following straight lines 2.5 km 45° north of west; then 4.70 km 60° south of east; then 5.1 km straight east; then 7.2 km 55 south of west; and finally 2.8 km 5 north of east. What is his final position in kilometers and degrees south of east relative to the island?

Answer 1

Answer:8.28 km

Explanation:

Given

First it drifts
`45^(\circ)` 2.5 km

`r_1=2.5cos45 i+2.5sin45 j`

Secondly it drifts
`60^(\circ)` 4.70 km

`r_(12)=4.7cos60 i-4.7sin60 j`

After that it drifted along east direction 5.1 km

`r_(23)=5.1 i`

After that it drifts
`55^(\circ)` 7.2 km

`r_(34)=-7.2cos55 i-7.2sin55 j`

After that it drifts
`5^(\circ)` 2.8 km

`r_(54)=-2.8cos5 i+2.8sin5 j`

`r_(5O)`=
`\left [ 2.5cos45+4.7cos60+5.1-7.2cos55-2.8cos5\right ]\hat{i}`+
`\left [ 2.5sin45-4.7sin60-7.2sin55+2.8sin5\right ]\hat{j}`

`r_(5O)=2.299\hat{i}-7.95\hat{j}`

`|r_(5O)|=8.28 km`

for direction

`tan\theta =(7.95)/(2.299)=3.4580`

`\theta =73.87^(\circ)` south of east

Answer 2

Step-by-step explanation:

Let us assume the direction east as i, direction west as -i, direction north as j and direction south as j.

Now, we define each of the straight lines as a vector with components along each of these unit vectors, we get

A : 2.5 km 45° north of west

A = 2.5 cos45 (-i) + 2.5 cos45 (j)

= -1.77(i) + 1.77(j)

B : 4.7 km 60° south of east

B = 4.7 cos60 (i) + 4.7 sin60 (-j)

= 2.35(i) - 4.07(j)

C : 5.1 km straight east

C = 5.1(i)

D : 7.2 km 55° south of west

D = 7.2 cos55 (-i) + 7.2 sin55 (-j)

= -4.13(i) - 5.9(j)

E: 2.8 km 5° north of east

E = 2.8 cos5 (i) + 2.8 sin5 (j)

= 2.79(i) + 0.24(j)

The resultant sum of all these vectors is as follows.

R = A + B + C + D + E

The sum of all the above yields,

R = 4.34(i) + 7.96(-j)

The magnitude of the resultant is as follows.

`|R| = \sqrt{4.34^(2) + (-7.96)^(2)}`

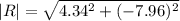
= 9.07

The angle that the resultant makes is as follows.

`\theta = tan^(-1)((7.96)/(4.34)) = 61.4^(o)`

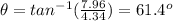
So, his final position relative to the island is as follows.

9.07 km, 61.4° south of east.

Thus, we can conclude that final position of Gilligan in kilometers and degrees south of east relative to the island is 9.07 km, 61.4° south of east.