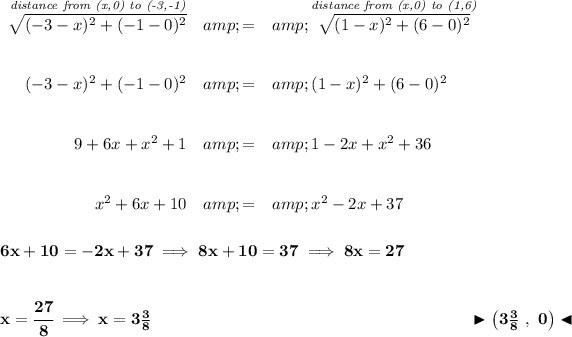Question

Find the point on the x-axis that is equidistant from the points (−3,−1) and (1,6)

Answer 1

well, we'll be using the distance formula twice here.

that point, is on the x-axis, what's the value of "y" at the x-axis? well y = 0, since it's way down at the 0 level, so the point must be (x , 0).

the distance then from (x,0) to (-3,-1) is the same distance as from (x,0) to 1,6).

`\bf \begin{array}{rcllll} \stackrel{\textit{distance from (x,0) to (-3,-1)}}{√((-3-x)^2+(-1-0)^2)}&=&\stackrel{\textit{distance from (x,0) to (1,6)}}{√((1-x)^2+(6-0)^2)} \\\\\\ (-3-x)^2+(-1-0)^2&=&(1-x)^2+(6-0)^2 \\\\\\ 9+6x+x^2+1&=&1-2x+x^2+36 \\\\\\ x^2+6x+10&=&x^2-2x+37 \end{array} \\\\\\ 6x+10=-2x+37\implies 8x+10=37\implies 8x=27 \\\\\\ x = \cfrac{27}{8}\implies x = 3(3)/(8)~\hfill \blacktriangleright \left( 3(3)/(8)~,~0 \right) \blacktriangleleft`