Answer:
(9.64 +- 0.86) m/s^2
Step-by-step explanation:
The generic motion equation for constant acceleration is
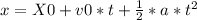
Where
X0: initial position
v0: initial speed
a: acceleration
t: time
If the object has an initial speed of zero, and the frame of reference is set conveniently so that the object initial position is zero, the equation simplifies to:
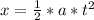
And the acceleration can be obtained as:

Where x is the distance fallen and a = g.
So, with the data x = (100.0 +- 0.03) mm and t = (144 +- 3) ms we can calculate
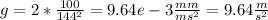
For the uncertainty we have to calculate the relative uncertainties first
For the distance (100 * 0.3)/100 = 0.3%
For the time (100 * 3)/144 = 2.08%
For multiplications or divisions the relative uncertainties are added
0.3% + 2.08% + 2.08% = 4.46%
We convert this into absolute uncertainty:
(9.64e-3 * 4.46)/100 = 0.00043 mm/(ms^2)
Finally, this is multiplied by a constant scalar, so:
2 * 0.00043 mm/(ms^2) = 0.00086 mm/(ms^2)
We convert the units
0.86 m/(s^2)
And the measurement is (9.64 +- 0.86) m/s^2
A better method is putting the ball in a ramp instead of a free fall, that way the fall is longer and the effect of time measuring uncertainty is reduced.