Question

Consider a Hydrogen atom with the electron in the n 8 shell. What is the energy of this system? (The magnitude of the ground state energy of the Hydrogen atom is 13.6 eV.) Submit Answer Tries 0/20 How many subshells are in this shell? Submit Answer Tries 0/20 How many electron orbits are in this main shell? Submit Answer Tries 0/20 How many electrons would fit in this main shell?

Answer 1

The energy of an electron in the 8th shell is given by: -0.2125 eV

The number of subshells is: 8

The number of orbitals is: 64

The number of electrons that fit on this shell is: 128

Step-by-step explanation:

First, we find the energy of the electrons in the 8th shell. In order to do this, we recall that the energy of an electron (in the Hydrogen atom) whose principal number is n is given by:

`E_(n)=-13.6(1)/(n^(2))`

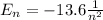
Substituting n=8, we find that the energy is given by:

`E_(8) = -13.6(1)/(8^(2))=-0.2125`

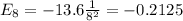
In order to find the number of subshells we recall that, for a given principal quantum number n, the possible values of the quantum number l, which corresponds to the number of subshells are:

0, 1, 2, ... , n-1

Since n = 8 in our problem, the possible values of l are: 0, 1, 2, 3, 4, 5, 6, 7. Therefore, the number of subshells are 8.

Now we continue with the number of orbitals. For every subshell l, we have 2l+1 possible values of m, which correspond to the orbitals. Since the possible values of l are: 0,1,2,3,4,5,6,7, therefore, we have to perform the sum:

`\sum_(l=0)^(7)(2l+1) = 8^2=64`

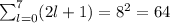
And we can conclude that the number of orbitals is equal to 64.

Finally, we know that we can fit two electrons per orbital, therefore we can have 64*2 = 128 electrons in the shell corresponding to n=8.