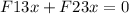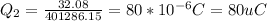Question

Two particles are fixed on an x axis. Particle 1 of charge 44.9 μC is cated at х- 24.5 cm; particle 2 of charge Q is located at x 7.53 cm. Particle 3 o charge magnitude 38.9 uc is released from rest on the y axis at y 24.5 cm, what is the value of Q if the initial acceleration of particle 3 is in the positive direction of (a) the x axis and (b) the y axis?

Answer 1

The force that is being exerted on particle 3 by particle 1 is equal to:

`F_(13)=(K*Q_1*Q_3)/(r13^2)`

`r_(13) = √((0.245m)^2 + (0.245m)^2)=0.3465m^2`

`F_(13)=(9*10^9Nm^2/C^2*44.9*10^-6C*38.9*10^-6C)/(0.3465m^2)=45.37N`

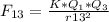
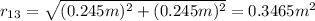
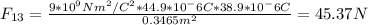
As both particles has positive charges, the particles will repel each other and the resultant force will have the direction of the vector
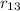`r_(13)`. Therefore,
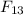`F_(13)` will have x and y components equal to:

`F{13x}=F{13}*(r13x)/(|r13|)=45.37N*(0.245m)/(0.3465m)=32.08 N`

`F{13y}=F{13}*(r13y)/(|r13|)=45.37N*(0.245m)/(0.3465m)=32.08 N`

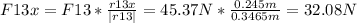
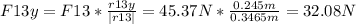
In order to calculate Force between particles 2 and 3, we first assume Q2 to be possitive (if it's negative the result will have a negative value, so this doesn't matter). We follow the same line of reasoning we used to calculate F13, just that Q2 will be unknown.

`F_(23)=(K*Q_2*Q_3)/(r13^2)`

`r_(23) = √((-0.0753m)^2 + (0.245m)^2)=0.2563m^2`

`F_(23)=(9*10^9Nm^2/C^2*Q_2*38.9*10^-6C)/(0.2563m^2)=1.36*10^6Q_2`

`F{23x}=F{23}*(r23x)/(|r23|)=1.36*10^6Q_2*(-0.0753m)/(0.2563m)= -401286.15Q_2`

`F{23y}=F{23}*(r23y)/(|r23|)=1.36*10^6Q_2*(0.245m)/(0.2563m)=1.305*10^6 Q_2`

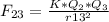
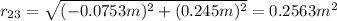
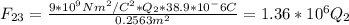
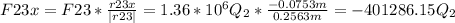
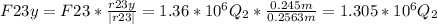
a) For incise a, F13y + F23y has to be equal to 0:

`F{13y}+F{23y}=0`

`32.08 N+1.305*10^6 Q_2=0`

`Q_2=(-32.08)/(1.305*10^6)=-24.6*10^(-6)C =-24.6uC`

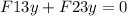
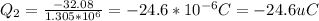
b) For incise b, F13x + F23x has to be equal to 0:

`F{13x}+F{23x}=0`

`32.08 N - 401286.15 Q_2=0`

`Q_2=(32.08)/(401286.15)=80*10^(-6)C =80uC`