Answer:
ST = 7.07 units
Explanation:
* Lets explain how to find the length of a segment
- The length of a segment whose endpoints are
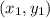
and
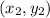 can be founded by the rule of the distance
can be founded by the rule of the distance
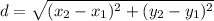
* Lets solve the problem
∵ The line segment is ST
∵ S is (-3 , 10)
∵ T is (-2 , 3)
- Assume that S is
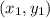 and T is
and T is
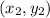
∴
 and
and

∴
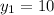 and
and
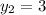
- By using the rule above
∴
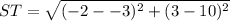
∴
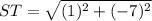
∴
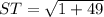
∴
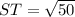
∴ ST = 7.07 units