Question

A current of 0,5A flows through a 22 resistor for 100s. The system who- se initial temperature is 300K is thermally isolated. The heat capacity of the resistor is 0,24JK-1 for a wide range of temperatures. The temperatu- re of the resistor changes appreciably. What is the entropy change of the system?

Answer 1

The entropy change of the system is 0.1265 J/K.

Step-by-step explanation:

Given that,

Current = 0.5 A

Resistor = 2 Ω

Time = 100 s

Temperature = 300 K

Heat capacity = 0.24 J/K

We need to calculate the heat produced

Using formula of heat

`H=i^2* R* t`

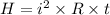
Where, i = current

R = resistor

t = time

Put the value into the formula

`H=0.5^2*2*100`

`H=50\ J`

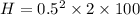
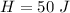
We need to calculate the change in temperature

Using formula of temperature

`\Delta T=(50)/(0.24)`

`\Delta T=208.33\ K`

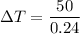
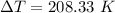
Now, The temperature is

`T_(2)=300+208.33=508.3\ K`

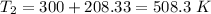
We need to calculate the entropy change of the system

Using formula of entropy

`\Delta S=\int_{T_(1)}^{T_(2)}{C(dT)/(T)}`

`\Delta S=C* ln((T_(2))/(T_(1)))`

`\Delta S=0.24* ln{(508.3)/(300)}`

`\Delta S=0.1265\ J/K`

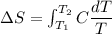
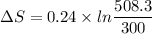
Hence, The entropy change of the system is 0.1265 J/K.