Question

An RLC circuit has resistance R = 205 ⦠and inductive reactance XL = 369 â¦. Calculate the circuit's capacitive reactance XC (in â¦) if its power factor is cos(Ï) = 1.00 â 10^â2.

Answer 1

Step-by-step explanation:

It is given that,

Resistance, R = 205 ohms

Inductive reactance,
`X_L=369\ \Omega`

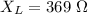
Power factor,
`cos\phi=10^(-2)`

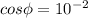
The power factor is given by :

`Cos\phi=(R)/(Z)`

R is the resistance of the circuit

Z is the impedance

We need to find the capacitive reactance of the circuit. Let it is
`X_c`.

`cos\phi=(R)/(√(R^2+(X_L-X_c)^2))`

`(10^(-2))/(205)=(1)/(√(R^2+(X_L-X_c)^2))`

`(X_L-X_c)^2=(1)/(2.37* 10^(-9))-R^2`

`(X_L-X_c)^2=(1)/(2.37* 10^(-9))-(205)^2`

`X_L-X_c=20540.17`

`X_c=20171.17\ \Omega`

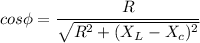
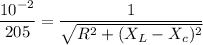
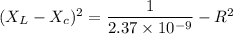
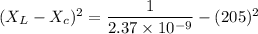
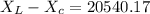
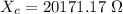
Hence, this is the required solution.