Answer:
The answer is 29,2368 m
Explanation:
In this case we have a right triangle and we know one side (in this case is the vertical side) and the measure of an angle different from the angle of 90 degrees, so we can solve this triangle, i.e. we can find the measure of any side (and of any angle too).
Remember that in a right triangle, labeled as in the question, we have that the vertical side is in fact the opposite leg of the angle A. So we have the following trigonometric ratio:
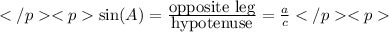
Solving the last equation for c we have
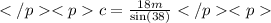
Using a calculator (don't forget to put the calculator in Deg mode) we have that the measure of the side c is 29,2368 m.