Question

Which of the following statements can be concluded (deducted) from the parallel-axis theorem? The area moment of inertia of an area about a noncentroidal axis is always less than that about a centroidal axis The area moment of inertia of an area about a noncentroidal axis is always greater than that about a centroidal axis The area moment of inertia of an area about a noncentroidal axis can be equal to that about a centroidal axis There is no relationship between the area moment of inertia of an area about a noncentroidal axis and that about a centroidal axis O None of the above

Answer 1

The statement that we can conclude is that the moment of inertial of any body about the centroidal axis is least of all the moment of inertia's of the body about any arbitrary axis in the body.

Step-by-step explanation:

According to parallel axis theorem we have

`I_(x)=I_(C.G)+Ax^(2)`

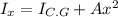
Where

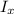`I_(x)` is the moment of inertia about any arbitrary axis.

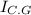`I_(C.G)` is the moment of inertia about centroidal axis.

A is the area of section of which Moment of area is evaluated

'x' = is the distance between the axis and C.G

thus we conclude that
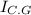`I_(C.G)` is least of all the moments.