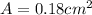Answers:
a)
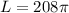
b)
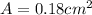
Explanation:
a) The area of the sector of a circle
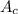 is given by:
is given by:
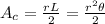 (1)
(1)
Where:
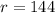 is the radius
is the radius
 is the length of arc
is the length of arc
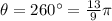 is the angle in radians (knowing
is the angle in radians (knowing
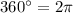 to make the conversion)
to make the conversion)
Isolating
 from (1) :
from (1) :
 (2)
(2)
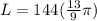 (3)
(3)
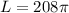 (4) This is the length of arc
(4) This is the length of arc
b) If we want to find the shaded area
 , we have to find the area of the sector of a circle
, we have to find the area of the sector of a circle
 and substract the area of the triangle
and substract the area of the triangle
 .
.
We already know
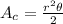 (5)
(5)
Where:

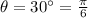 (remembering
(remembering
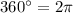 )
)
Hence:
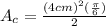 (6)
(6)
 (7) area of the sector of the circle
(7) area of the sector of the circle
On the other hand, the area of a triangle is given by:
 (8)
(8)
Where:
 is the base of the triangle
is the base of the triangle
 is the height of the triangle
is the height of the triangle
If we divide this triangle in half, we will have two right triangles, each one with a height
 and a base
and a base
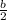 , and hypotenuse=4cm.
, and hypotenuse=4cm.
In addition, each triangle will have the following angles (in degrees):
 ,
,
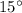 (the half of
(the half of
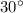 ),
),
 (knowing the three inner angles of a triangle sum to
(knowing the three inner angles of a triangle sum to
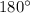 ).
).
Having this clear, let's use the trigonometric functions sine and cosine to find the values of
 and
and
 :
:
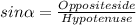 (9)
(9)
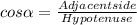 (10)
(10)
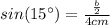 (11)
(11)
 (12) This is the base of the triangle
(12) This is the base of the triangle
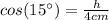 (13)
(13)
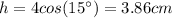 (14) This is the height of the triangle
(14) This is the height of the triangle
Substituting (12) and (14) in (8):
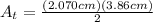 (15)
(15)
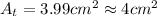 (16) This is the area of the triangle
(16) This is the area of the triangle
Substracting the area of the triangle from the area of the sector of the circle:
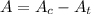 (17)
(17)
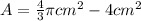 (18)
(18)
Finally we have the area of the shaded portion: