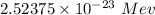Question

Estimate the uncertainty in energy during a time interval of 10-23 s. Express your answer in MeV

Answer 1

The uncertainty in energy during a time interval is
`2.52375*10^(-23)\ Mev`

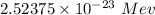
Step-by-step explanation:

Given that,

Time
`\Delta t= 10-23= 13 s`

We need to calculate the uncertainty in energy

Using uncertainty principle

`\Delta E \Delta t \geq (\hbar)/(2)`

`\Delta E \geq(\hbar)/(2\Delta t)`

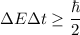
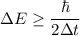
Put the value into the relation

`\Delta E=(1.05*10^(-34))/(2*13)`

`\Delta E\geq 4.038*10^(-36)\ J`

`\Delta E\geq (4.038*10^(-36))/(1.6*10^(-19))`

`\Delta E\geq 2.52375*10^(-17)\ ev`

`\Delta E\geq(2.52375*10^(-17))/(10^(6))\ MeV`

`\Delta E\geq 2.52375*10^(-23)\ Mev`

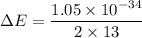
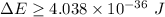
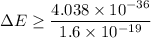
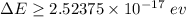
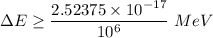
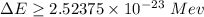
Hence, The uncertainty in energy during a time interval is
`2.52375*10^(-23)\ Mev`