Question

A hungry fish is about to have lunch at speeds shown. Assume the hungry fish has a mass five times the mass of the small fish. Immediately after lunch, rank from greatest to least the speeds of the formerly hungry fish.

a) Big: v=4m/s, little: 0
b) Big: v=4m/s, little:1 m/s
c) Big: v=5 m/s, little: 2 m/s

Answer 1

The answer is C > A > B

Explanation:

This a conservation of momentum problem, that means that the initial momentum of the system is equal to final momentum of the system.

The mass of the big fish is 5 times greater than the mass of the smaller fish, therefore, to make things simpler,

Let the mass of the big fish be 5 kg and the mass of the small one be 1 kg.

In our case we have:

Momentum before lunch = momentum after lunch.

`(v_(1) *m_(1)) + (v_(2) *m_(2)) = (m_(1) *m_(2))* v\\`

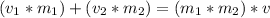
In the first case (A), v1 = 4 m/s ; v2 = 0 m/s

(4 m/s*5kg) + (0 m/s*1 kg) = (5kg + 1 kg)*v

20 + 0 = 6v

V =
`(20)/(6)`

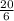
V =
`(10)/(3)` m/s

In the second case (B), v1 = 4 m/s ; v2 = -1 m/s (v2 is negative because it’s going to the opposite direction of the bigger fish)

(4 m/s*5kg) + (-1 m/s*1 kg) = (5kg + 1 kg)*v

20 - 1 = 6v

V =
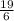`(19)/(6)` m/s

In the third case (C), v1 = 5 m/s ; v2 = -2 m/s (v2 is negative because it’s going to the opposite direction of the bigger fish)

(5 m/s*5kg) + (-2 m/s*1 kg) = (5kg + 1 kg)*v

25 - 2 = 6v

V =
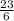`(23)/(6)` m/s

Therefore, the greatest speed is the third case and the smallest is the second case. So, C > A > B