Question

Please help me! 90 points!

The equation shown below has exactly one solution.

−5x + 3 = 2(x + 1)

Step 1: Change the equation so it has no solutions.

Step 2: Change your equation from Step 1 so it has infinitely many solutions.

Rules
1. All equations must be linear and have only variable, x

2. You can make one—and only one—of the following changes to each equation:
o Change one term.
o Delete one term.
o Add one term.

What are your equations?

Explain how you know each equation has one, none, or infinitely many solutions.

Answer 1

1/7

Explanation:

Answer 2

To make it so that the equations have no solutions, we have to make the x's cancel out.

Lets do this by changing -5 into 2.

Equation 1;

`2x+3=2(x+1)`

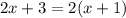
This works, because when we expand the brackets, we get 2x + 1 on the right side. Then when we subtract 2x from both sides to try and solve the equation, we end up cancelling out all of the x's, leaving us with 3=2. And since 3 does not equal 2, hence there are no solutions

______________________

To make an equation have an infinite amount of solutions, we have to make both sides (the left and right) be exactly the same.

We can do this by changing the 3 in our equation above into 2:

Equation 2:

`2x+2=2(x+1)`

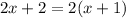
No matter what we say what x is, both sides of the equation will be the same, and cancel down to 0.

In that equation, x could be 0, or 1 or 2 or 324 or 2041 or any other number (hence any infinite number of solutions)

__________________

Explanation for the equation with only one solution:

It only has one solution, because there is only one value for x that makes the equal sign correct..

-5x + 3 = 2(x + 1)

If we solve it we get that x = 1/7.

If we substitute in 1/7 into x, we get:

-5(1/7) + 3 = 2(1/7 + 1)

-5/7 + 3 = 2/7 +2

16/7 = 16/7 (now the equal sign is correct)

But if we substitute in other number, like 3, the equal sign won't be true.

1/7 is the only number that can be substituted into x to make the equation 'correct'. Hence, there is only one solution