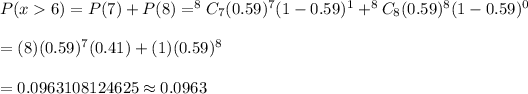Answer: (1) 0.1332
(2) 0.0963
Explanation:
Given : The proportion of US adults have little confidence in their cars:p = 0.59
Sample size : n= 8
Using Binomial probability formula :-
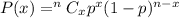
Then, the probability that the number of US adults who have little confidence in their cars is exactly three :-
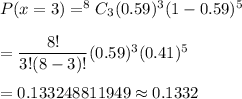
The probability that the number of US adults who have little confidence in their cars is more than 6:-