Question

Eric is studying people's typing habits. He surveyed 525 people and asked whether they leave one space or two spaces after a period when typing. 440 people responded that they leave one space. Create a 90% confidence interval for the proportion of people who leave one space after a period.

Answer 1

Answer:
`(0.81155,\ 0.86445)`

Explanation:

The confidence interval for population proportion (p) is given by :_

`\hat{p}\pm z^* \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

, where n= sample size

z* = Critical value.

`\hat{p}` = Sample proportion.

Let p be the true population proportion of people who leave one space after a period.

As per given , we have

n= 525

`\hat{p}=(440)/(525)=0.838`

By z-table , the critical value for 90% confidence interval : z* = 1.645

Now , 90% confidence interval for the proportion of people who leave one space after a period:

`0.838\pm (1.645) \sqrt{(0.838(1-0.838))/(525)}`

`0.838\pm (1.645) √(0.00025858)`

`0.838\pm (1.645) (0.0160805117)`

`\approx0.838\pm(0.02645)`

`=(0.838-0.02645,\ 0.838+0.02645)=(0.81155,\ 0.86445)`

Hence, a 90% confidence interval for the proportion of people who leave one space after a period.
`=(0.81155,\ 0.86445)`

Answer 2

The confidence interval is (0.81, 0.87).

Explanation:

There's 90% confidence that population proportion is within the interval obtained from the following formula:

`\hat{p}\pm z_(\alpha/2)\sqrt{\frac{\hat{p}*(1-\hat{p})}{n}}`

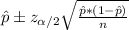
Knowing that the sample size,
`n=525` we obtain the proportion of people from the sample who leave one space after a period as
`\hat{p}=(440)/(525)=0.8381\approx 0.84`.

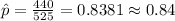We then look for the critical value:

`z_(\alpha/2)=1.645`

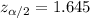
Now we can replace in the formula to obtain the confidence interval:

`0.84\pm 1.645\sqrt{(0.84*(1-0.84))/(525)}= (0.8137; 0.8663)`

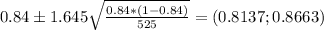
Therefore we can say that there's 90% probability that the population proportion of people who leave one space after a period lies between the values (0.8137; 0.8663).