Answer:
The dimensions are, base
![b=\sqrt[3]{200}](https://img.qammunity.org/2020/formulas/mathematics/college/46vto459roal5wptkhw9utnrx37pjjjqla.png) , depth
, depth
![d=\sqrt[3]{200}](https://img.qammunity.org/2020/formulas/mathematics/college/358tmkggn3lcnx2anayfzdblhbpaikc11z.png) and height
and height
![h=\sqrt[3]{200}](https://img.qammunity.org/2020/formulas/mathematics/college/aczy05brz9zmyzumwnanauc8t48ir3zae6.png) .
.
Explanation:
First we have to understand the problem, we have a box of unknown dimensions (base
 , depth
, depth
 and height
and height
 ), and we want to optimize the used material in the box. We know the volume
), and we want to optimize the used material in the box. We know the volume
 we want, how we want to optimize the card used in the box we need to minimize the Area
we want, how we want to optimize the card used in the box we need to minimize the Area
 of the box.
of the box.
The equations are then, for Volume
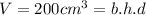
For Area
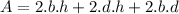
From the Volume equation we clear the variable
 to get,
to get,
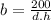
And we replace this value into the Area equation to get,
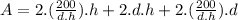
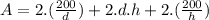
So, we have our function
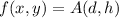 , which we have to minimize. We apply the first partial derivative and equalize to zero to know the optimum point of the function, getting
, which we have to minimize. We apply the first partial derivative and equalize to zero to know the optimum point of the function, getting
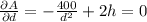
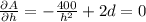
After solving the system of equations, we get that the optimum point value is
![d=\sqrt[3]{200}](https://img.qammunity.org/2020/formulas/mathematics/college/358tmkggn3lcnx2anayfzdblhbpaikc11z.png) and
and
![h=\sqrt[3]{200}](https://img.qammunity.org/2020/formulas/mathematics/college/aczy05brz9zmyzumwnanauc8t48ir3zae6.png) , replacing this values into the equation of variable
, replacing this values into the equation of variable
 we get
we get
![b=\sqrt[3]{200}](https://img.qammunity.org/2020/formulas/mathematics/college/46vto459roal5wptkhw9utnrx37pjjjqla.png) .
.
Now, we have to check with the hessian matrix if the value is a minimum,
The hessian matrix is defined as,
![H=\left[\begin{array}{ccc}(\partial^2 A)/(\partial d^2) &(\partial^2 A)/(\partial d \partial h)\\(\partial^2 A)/(\partial h \partial d)&(\partial^2 A)/(\partial p^2)\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/hwmwfh5sufkf9azfw4p3qvdo8mmw04nppx.png)
we know that,
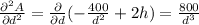

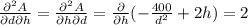
Then, our matrix is
![H=\left[\begin{array}{ccc}4&2\\2&4\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/u51a1ow50qrc7pltsjorcmv0x5y5uirqt6.png)
Now, we found the eigenvalues of the matrix as follow
![det(H-\lambda I)=det(\left[\begin{array}{ccc}4-\lambda&2\\2&4-\lambda\end{array}\right] )=(4-\lambda)^2-4=0](https://img.qammunity.org/2020/formulas/mathematics/college/85ml4ifpqhtwcyx1ntdhbc8fe1mv7o6x6l.png)
Solving for
 , we get that the eigenvalues are:
, we get that the eigenvalues are:
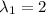 and
and
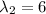 , how both are positive the Hessian matrix is positive definite which means that the function
, how both are positive the Hessian matrix is positive definite which means that the function
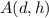 is minimum at that point.
is minimum at that point.