Question

Assume that blood pressure readings are normally distributed with a mean of 118 and a standard deviation of 6.4. If 64 people are randomly​ selected, find the probability that their mean blood pressure will be less than 120. Round to four decimal places. A. 0.9938 B. 0.8615 C. 0.9998 D. 0.0062

Answer 1

Option A - 0.9938

Explanation:

Given : Assume that blood pressure readings are normally distributed with a mean of 118 and a standard deviation of 6.4. If 64 people are randomly​ selected.

To find : The probability that their mean blood pressure will be less than 120?

Solution :

The formula to find the probability is

`P(Z=X)=(X-\mu)/((\sigma)/(√(n)))`

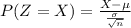
Where, X is the sample mean

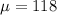`\mu=118` is the population mean

`\sigma=6.4` is the standard deviation

n=64 is the number of sample

The probability that their mean blood pressure will be less than 120 is given by,

`P(Z<120)=(120-118)/((6.4)/(√(64)))`

`P(Z<120)=(2)/((6.4)/(8))`

`P(Z<120)=(2)/(0.8)`

`P(Z<120)=2.5`

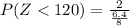
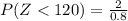
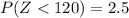
From the z-table the value of z at 2.5 is

`P(Z<120)=0.9938`

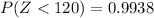
Therefore, Option A is correct.

The probability that their mean blood pressure will be less than 120 is 0.9938.