Answer:
(a) 1.5 second
(b) 0.56 m
Step-by-step explanation:
Pendulum makes 120 oscillations in 3 min that means in 180 seconds
time taken by the pendulum to complete one oscillation is called time period.
(a) So, the time period is 180 / 120 = 1.5 second
T = 1.5 second
Thus, the time period of the pendulum is 1.5 second.
(b) g = 9.8 m/s^2
The formula for the time period is given by
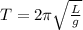
Where, L be the length of pendulum
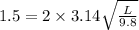
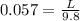
L = 0.56 m
Thus, the length of the pendulum is 0.56 m .