Question

A company produces two types of solar panels per year: x thousand of type A and y thousand of type B. The revenue and cost equations, in millions of dollars, for the year are given as follows. R(x, y)-5x + 7y C(x,y) x2-2xy+9y+3x -87y-6 Determine how many of each type of solar panel should be produced per year to maximize proft. The company will achieve a maximum profit by selling solar panels of type A and sellingsolar panels of type B

Answer 1

• 7000 type A
• 6000 type B

Explanation:

We assume your equations are intended to be ...

`C(x,y)=x^2-2xy+9y^2+3x-87y-6\\R(x,y)=5x+7y`

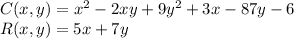
Then the profit equation is ...

`P(x,y)=R(x,y)-C(x,y)=5x+7y-x^2+2xy-9y^2-3x+87y+6\\=-x^2+2xy-9y^2+2x+94y+6`

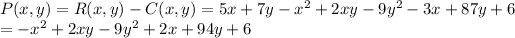
The partial derivatives of profit with respect to x and y are zero when profit is maximized.

∂P/∂x = 0 = -2x +2y +2

∂P/∂y = 0 = 2x -18y +94

Simplifying, these equations are ...

• y = x -1
• x -9y = -47

Substituting the first into the second gives ...

x -9(x -1) = -47

-8x = -56

x = 7

y = 7 -1 = 6

The company will maximize profit by selling 7000 panels of type A and 6000 panels of type B.