Answer: 0.7030
Explanation:
Given : The population proportion for company's orders come from first-time customers : p=0.43
Sample size : n= 98
The test statistic for population proportion:-
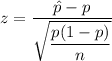
For ,
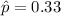
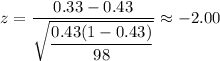
For ,
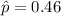
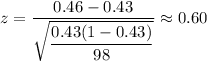
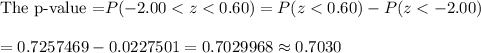
Hence, the probability that the sample proportion is between 0.33 and 0.46 is 0.7030.