Question

A 3-kg rock is thrown upward with a force of 200 N at a location where the local gravitational acceleration is 9.79 m/s2 . Determine the acceleration of the rock, in m/s

Answer 1

Answer:
`56.87m/s^(2)`

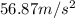
Step-by-step explanation:

If we make an analysis of the net force
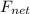`F_(net)` of the rock that was thrown upwards, we will have the following:

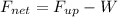`F_(net)=F_(up)-W` (1)

Where:

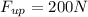`F_(up)=200N` is the force with which the rock was thrown

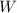`W` is the weight of the rock

Being the weight the relation between the mass
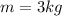`m=3kg` of the rock and the acceleration due gravity
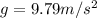`g=9.79m/s^(2)` :

`W=m.g=(3kg)(9.79m/s^(2))` (2)

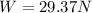`W=29.37 N` (3)

Substituting (3) in (1):

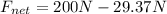`F_(net)=200N-29.37 N` (4)

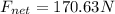`F_(net)=170.63 N` (5) This is the net Force on the rock

On the other hand, we know this force is equal to the multiplication of the mass with the acceleration, according to Newton's 2nd Law:

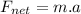`F_(net)=m.a` (6)

Finding the acceleration
`a`:

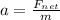`a=(F_(net))/(m)` (7)

`a=(170.63 N)/(3kg)` (8)

Finally:

`a=56.87m/s^(2)`