Question

Suppose a mutual fund qualifies as having moderate risk if the standard deviation of its monthly rate of return is less than 6​%. A​ mutual-fund rating agency randomly selects 25 months and determines the rate of return for a certain fund. The standard deviation of the rate of return is computed to be 5.61​%. Is there sufficient evidence to conclude that the fund has moderate risk at the alpha = 0.10 level of​ significance? A normal probability plot indicates that the monthly rates of return are normally distributed.

Answer 1

With a 0.1 significance level, there is not sufficient evidence to state that the fund has a moderate risk.

Explanation:

To solve this problem, a variance hypothesis test is run.

Null hypothesis variance (PV) = 36

Sample size (n) = 25

Sample variance (SV) = (5.61)^2 = 31.4721

Significance level = 0.1

H0: PV = 36

Ha: PV
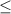`\leq` 36

Test statistic = (n-1) SV / PV

Calculated statistic = (24) (31.4721) / 36 = 20.9814

Critical chi-square value = 15.6587

Since, Calculated statistic is greater than or equal to Chi-square critical value, the null hypothesis cannot be rejected. There is not sufficient evidence to state that the fund has a moderate risk.