Answer:
The x-coordinate of the parabola's vertex is 6.
Explanation:
A parabola in the following format:
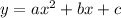
With
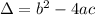
Has the following vertex:
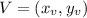
In which
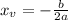
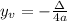
In this problem, we have that:
A parabola intersects the x-axis at x = 3 and x = 9. This means that the roots are x = 3 and x = 9, and that our parabola is defined by the following equation:
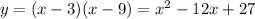
So

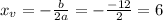
The x-coordinate of the parabola's vertex is 6.