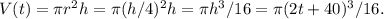Answer:
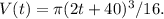
Explanation:
Assuming that height
 is a function of time, we have to
is a function of time, we have to
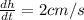 . Integrating
. Integrating
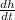 and applying the first fundamental theorem of the calculation you get:
and applying the first fundamental theorem of the calculation you get:
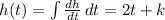 . Since
. Since
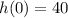 , you have to
, you have to
 and therefore,
and therefore,
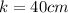 and
and
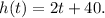
Now, if diameter is always half its height,
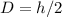 or what is equal
or what is equal
 . With all this,
. With all this,