Answer:
The values of x and y, x = 9.5 , y = 19.5
Explanation:
* Lets explain how to solve the problem
∵ Points P , Q and M are collinear
∵ Point Q divides JM where JQ : QM = 2/3
∵ Point J is located at (2 , 7)
∵ Point Q is located at (5 , 12)
∵ Point M is located at (x , y)
- The rule of the point of division is:
its x-coordinate =
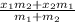
its y-coordinate =
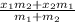
where
 and
and
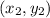 are the
are the
endpoints of the segment and
 ,
,
 are
are
the parts of the ratio
* Lets solve the problem
∵ Q is the point of the division
∵ J is

∵ M is
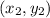
∵
 = 2 and
= 2 and
 = 3
= 3
∴
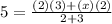
∴
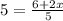
- Multiply both sides by 5
∴ 25 = 6 + 2x
- Subtract 6 from both sides
∴ 19 = 2x
- Divide both sides by 2
∴ x = 9.5
∴
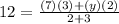
∴
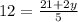
- Multiply both sides by 5
∴ 60 = 21 + 2y
- Subtract 6 from both sides
∴ 39 = 2y
- Divide both sides by 2
∴ y = 19.5
* The values of x and y are x = 9.5 and y = 19.5
∵ Point M located at (x , y)
∴ Point M located at (9.5 , 19.5)