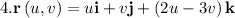Answer:
1. B
2. C
3. A
4. D
Explanation:
The parametric equations of the circular cylinder are:
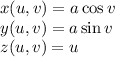
If the orientation of the cylinder is changed to have the height
 along the x-axis, the parametric equations of the cylinder match:
along the x-axis, the parametric equations of the cylinder match:
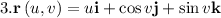
The parametric equations of the circular paraboloid are:
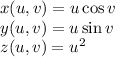
Using the units vectors the parametric equations match:
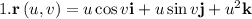
The parametric equations of the cone are:
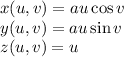
Using the units vectors and rotating the base of the cone from
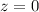 to
to
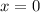 the parametric equations match:
the parametric equations match:
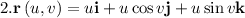
The equation left is the equation of a plane: