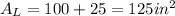Question

Find the lateral area of this square

based pyramid.

10 in

Sin

[ ? Jin?

Answer 1

`A_(L) =125 in^(2)`

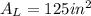
Explanation:

Let's break down the pyramid in different bidimensional figures. As you can see in the image, the pyramid has 5 total sides: 4 of them are triangles and 1 is a square (the bottom). Therefore, the total area of this pyramid is given by the area of 4 triangles of base 5 in and height 10 in, and a square whose sides measure 5 in.

1. Write an expression and find the area of all triangles.

We already know the formula for the area of a triangle:
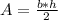`A=(b*h)/(2)`, where b is the measure of the base of the triangle, and h is the height is the triangle. We have 4 triangles, therefore, let's multiply this formula by 4 and calculate.

`A=4*((b*h)/(2))=\\ \\ \\A=4*(((5)(10))/(2))=\\ \\A=4*((50)/(2))=\\ \\A=4*(25)=\\ \\A=100`

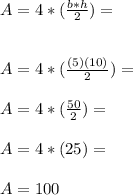
2. Find the area of the bottom side.

The bottom side is a square whose whose sides measure 5 in. Hence, it's area is:

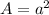`A=a^(2)`, where a is the length of one side. Then:

`A=(5)^(2)\\ \\A=25`

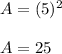
3. Add up all the areas to get the total alteral area of this pyramid.

`A_(L) =100+25=125 in^(2)`