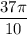Answer:
The volume is:
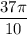
Step-by-step explanation:
See the sketch of the region in the attached graph.
We set the integral using washer method:
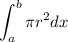
Notice here the radius of the washer is the difference of the given curves:
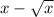
So the integral becomes:
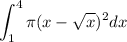
We solve it:
Factor
 out and distribute the exponent (you can use FOIL):
out and distribute the exponent (you can use FOIL):
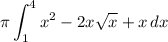
Notice:
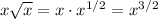
So the integral becomes:
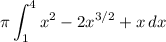
Then using the basic rule to evaluate the integral:

Simplifying a bit:
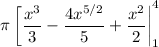
Then plugging the limits of the integral:
![\displaystyle\pi\left[(4^3)/(3)-(4(4)^(5/2))/(5)+(4^2)/(2)-\left((1)/(3)-(4)/(5)+(1)/(2)\right)\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/g6dvzjh2z4v4k10ju2w3drj9xsojknhlh5.png)
Taking the root (rational exponents):
![\displaystyle\pi\left[(4^3)/(3)-(4(2)^(5))/(5)+(4^2)/(2)-\left((1)/(3)-(4)/(5)+(1)/(2)\right)\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/hfz4v3t6ujmihi37b181nfznmps7trumjd.png)
Then doing those arithmetic computations we get: