Answer: (0.3751,0.4821)
Explanation:
Given : Level of significance :

Then , significance level :
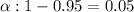
Since , sample size :
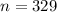 , i.e. a large sample (n<30).
, i.e. a large sample (n<30).
Then we use z-test.
Using excel (by going in formulas for more statistics and then statistics), Critical value :
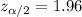
Also, the proportion of people said that they were fans of the visiting team :-
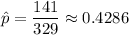
The confidence interval for population proportion is given by :-
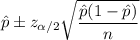

Hence, a 95% confidence interval for the population proportion of attendees who were fans of the visiting team= (0.3751,0.4821)