Question

The average rate of change of a function f(x)f from x=a to x=b is the slope of the line which passes through (a,f(a) and (b,f(b)). Consider the function f(x)=x^2+6 and find the following: (a) The average rate of change of f(x) from x=−1 to x=4. (b) The average rate of change of f(x) from x=a to x=b. (c) The average rate of change of f(x)f between the points (x,f(x)) and (x+h,f(x+h)). Assume h>0

Answer 1

a) 3

b) b + a

c) 2x + h

Explanation:

Since, The average rate of change of a function f(x)f from x=a to x=b is the slope of the line which passes through (a,f(a) and (b,f(b)), we can write the formula for Average Rate of Change as:

`(f(b)-f(a))/(b-a)`

Part a)

`f(x) = x^(2)+6`

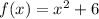
The average rate of change of f(x) from x = −1 to x = 4. Using these values in above formula, we get:

`(f(4)-f(-1))/(4-(-1))\\\\ =((4)^(2)+6-[(-1)^(2)+6])/(4+1)\\\\ =(16+6-1-6)/(5)\\\\ =(15)/(5)\\\\ =3`

Thus, the average rate of change of f(x) from x = −1 to x = 4 is 3

Part b)

The average rate of change of f(x) from x=a to x=b. Using the values in the above formula, we get:

`(f(b)-f(a))/(b-a)\\\\ = (b^(2)+6-a^(2)-6)/(b-a)\\\\ =(b^(2)-a^(2))/(b-a)\\\\ =((b-a)(b+a))/(b-a)\\\\ =b+a`

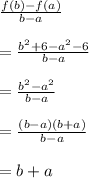
Thus, the average rate of change of f(x) from x = a to x = b is b + a

Part c)

The average rate of change of f(x) between the points (x,f(x)) and (x+h,f(x+h)). Using the values in above formula, we get:

`(f(x+h)-f(x))/(x+h-x)\\\\ =((x+h)^(2)+6-x^(2)-6)/(h)\\\\ =((x+h)^(2)-x^(2))/(h)\\\\ =(x^(2)+h^(2)+2xh-x^(2))/(h)\\\\ =(h^(2)+2xh)/(h)\\\\ =(h(h+2x))/(h)\\\\ = h + 2x`

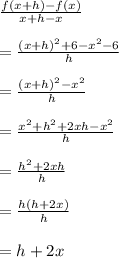
Thus, The average rate of change of f(x) between the points (x,f(x)) and (x+h,f(x+h)) is 2x + h.